Wariancja jest kluczowym pojęciem w analizie danych, które pomaga zrozumieć, jak bardzo różnią się wartości w danym zbiorze danych. W programie Excel istnieje kilka funkcji, które umożliwiają obliczenie wariancji, w zależności od rodzaju danych, które posiadasz. W tym artykule dowiesz się, jak skutecznie korzystać z funkcji takich jak VAR.S i VAR.P, aby obliczyć wariancję dla próbki lub całej populacji.
Obliczanie wariancji w Excelu jest proste i intuicyjne. Wystarczy wpisać odpowiednią funkcję w pustą komórkę, a Excel automatycznie przeprowadzi obliczenia na podstawie danych, które mu dostarczysz. W ten sposób możesz szybko uzyskać informacje o rozkładzie danych i ich zmienności, co jest niezwykle przydatne w analizie statystycznej.
Kluczowe wnioski:- Funkcja VAR.S służy do obliczania wariancji próbki, idealna, gdy masz dane z próby.
- Funkcja VAR.P oblicza wariancję dla całej populacji, gdy dysponujesz pełnym zestawem danych.
- Funkcja WARIA uwzględnia tekst i wartości logiczne, traktując tekst jako 0.
- Funkcja WARPA działa podobnie jak VAR.P, ale także uwzględnia tekst i wartości logiczne.
- Starsze funkcje VAR i WARIANCJA są dostępne dla zachowania zgodności, ale mogą być usunięte w przyszłych wersjach Excela.
- Aby obliczyć wariancję, wystarczy wpisać funkcję w komórkę, np. =VAR.S(A1:A10), gdzie A1:A10 to zakres danych.
Jak obliczyć wariancję w Excelu - krok po kroku dla początkujących
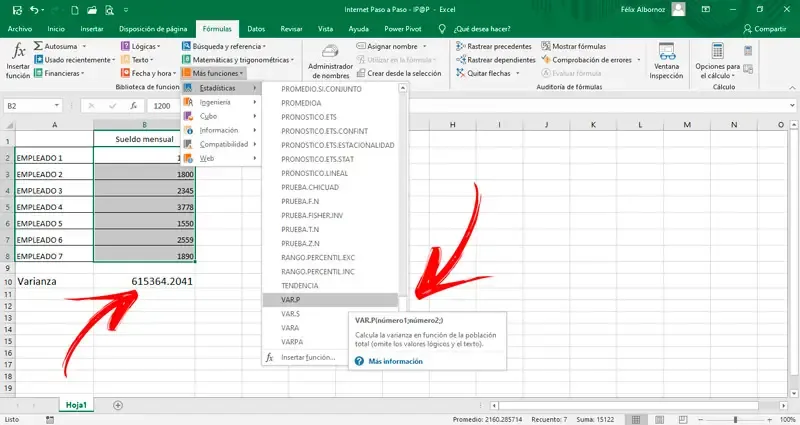
Obliczanie wariancji w Excelu jest prostym procesem, który można zrealizować przy użyciu kilku podstawowych funkcji. Aby rozpocząć, należy mieć dane, dla których chcemy obliczyć wariancję, wprowadzając je do odpowiednich komórek arkusza kalkulacyjnego. Najczęściej używane funkcje do obliczania wariancji to VAR.P dla całej populacji oraz VAR.S dla próby. Wybór odpowiedniej funkcji jest kluczowy, ponieważ zależy od tego, czy dysponujemy pełnym zbiorem danych, czy tylko próbą.Po zdefiniowaniu danych, wystarczy wpisać odpowiednią funkcję w pustą komórkę, na przykład =VAR.S(A1:A10), gdzie A1:A10 to zakres komórek z danymi. Po naciśnięciu klawisza Enter, Excel obliczy wariancję, a wynik zostanie wyświetlony w wybranej komórce. To proste podejście sprawia, że obliczanie wariancji w Excelu jest dostępne nawet dla początkujących użytkowników, którzy chcą szybko analizować swoje dane.
Jak korzystać z funkcji VAR.P i VAR.S w Excelu
Funkcje VAR.P i VAR.S w Excelu służą do obliczania wariancji, ale różnią się one zastosowaniem. VAR.P jest używana, gdy mamy do czynienia z pełną populacją danych, co oznacza, że wszystkie dostępne wartości są uwzględnione w obliczeniach. Z kolei VAR.S jest przeznaczona do obliczania wariancji na podstawie próbki, czyli podzbioru danych, co jest szczególnie przydatne w analizach statystycznych, gdzie pracuje się na ograniczonej liczbie obserwacji.
Aby użyć tych funkcji, wystarczy wpisać odpowiednią formułę w komórkę. Na przykład, aby obliczyć wariancję próbki dla danych znajdujących się w komórkach A1 do A10, należy wpisać =VAR.S(A1:A10). Dla pełnej populacji, używamy =VAR.P(A1:A10). Po naciśnięciu klawisza Enter, Excel obliczy wariancję i wyświetli wynik w wybranej komórce.
| Funkcja | Opis | Kiedy używać |
|---|---|---|
| VAR.P | Oblicza wariancję dla całej populacji. | Gdy masz pełne dane, np. wyniki wszystkich uczniów w klasie. |
| VAR.S | Oblicza wariancję dla próbki danych. | Gdy pracujesz na próbie, np. wyniki testów 10 uczniów z całej klasy. |
Praktyczne przykłady obliczania wariancji w Excelu
Obliczanie wariancji w Excelu można zrealizować na wiele sposobów, ale kluczowe jest, aby mieć odpowiednie dane. Na przykład, jeśli mamy zestaw danych dotyczących wyników egzaminów uczniów w klasie, możemy obliczyć wariancję, aby zrozumieć, jak bardzo wyniki różnią się od średniej. Załóżmy, że mamy następujące wyniki: 85, 90, 78, 92, 88. Aby obliczyć wariancję dla tej populacji, użyjemy funkcji VAR.P, co pozwoli nam uzyskać pełen obraz rozkładu wyników.
W przypadku tego zestawu danych, wprowadzamy wyniki do komórek A1 do A5, a następnie w komórce A6 wpisujemy formułę =VAR.P(A1:A5). Po naciśnięciu Enter, Excel zwróci wartość wariancji, która informuje nas, jak bardzo różnią się wyniki uczniów od średniej. Tego typu analizy są niezbędne w edukacji, aby ocenić, czy uczniowie osiągają podobne wyniki, czy też są znaczne odchylenia, które wymagają dalszej analizy.
Obliczanie wariancji dla zestawu danych z populacji
Rozważmy konkretny przykład obliczania wariancji dla zestawu danych z populacji. Mamy dane dotyczące liczby sprzedanych egzemplarzy książek w ciągu tygodnia w pięciu różnych księgarniach: 120, 135, 150, 165, 140. Umieszczamy te wartości w komórkach B1 do B5. Aby obliczyć wariancję dla tej populacji, w komórce B6 wpisujemy formułę =VAR.P(B1:B5). Po naciśnięciu Enter, Excel obliczy wariancję, co pozwoli nam ocenić, jak bardzo sprzedaż różni się w poszczególnych księgarniach.
Obliczanie wariancji dla zestawu danych z próby
Aby obliczyć wariancję dla zestawu danych z próby w Excelu, możemy użyć funkcji VAR.S. Załóżmy, że mamy dane dotyczące wyników testu przeprowadzonego na grupie 10 studentów, których wyniki to: 75, 82, 88, 90, 76, 85, 93, 78, 81, 87. Wprowadzamy te wartości do komórek C1 do C10. Następnie, aby obliczyć wariancję próbki, w komórce C11 wpisujemy formułę =VAR.S(C1:C10). Po naciśnięciu Enter, Excel obliczy wariancję, co pozwoli nam zrozumieć, jak zróżnicowane są wyniki studentów w tej próbie.
Najczęstsze błędy przy obliczaniu wariancji i jak ich unikać
Podczas obliczania wariancji w Excelu użytkownicy często popełniają pewne błędy, które mogą prowadzić do nieprawidłowych wyników. Jednym z najczęstszych błędów jest używanie niewłaściwej funkcji do obliczenia wariancji, np. stosowanie VAR.P zamiast VAR.S w przypadku danych z próby. Innym problemem jest pominięcie niektórych wartości w zakresie danych, co może zafałszować wynik. Ważne jest również, aby upewnić się, że dane nie zawierają błędów, takich jak tekst w komórkach, które powinny zawierać tylko liczby. Aby uniknąć tych problemów, zawsze warto dokładnie sprawdzić dane przed przystąpieniem do obliczeń.
- Użycie niewłaściwej funkcji dla danych z próby lub populacji.
- Pominięcie wartości w zakresie, co prowadzi do niepełnych obliczeń.
- Obecność tekstu lub błędnych danych w zakresie liczbowym.
Jak interpretować wyniki obliczeń wariancji w kontekście danych
Interpretacja wyników obliczeń wariancji jest kluczowa dla analizy danych. Wysoka wariancja wskazuje na dużą rozbieżność wyników, co może sugerować, że dane są zróżnicowane lub że istnieją czynniki wpływające na wyniki. Z kolei niska wariancja oznacza, że wyniki są bardziej jednorodne i bliskie średniej. Zrozumienie, co oznaczają te wyniki, pozwala na lepsze podejmowanie decyzji w kontekście analizy danych. W praktyce, analiza wariancji może pomóc w identyfikacji trendów oraz w podejmowaniu decyzji opartych na danych.
Czytaj więcej: Jak dodać procent w Excelu: Prosta formuła i przykłady
Jak wykorzystać wariancję do optymalizacji procesów biznesowych
Wariancja nie tylko pomaga w analizie danych, ale również może być kluczowym narzędziem w optymalizacji procesów biznesowych. Przykładowo, firmy mogą wykorzystać obliczenia wariancji do identyfikacji i eliminacji nieefektywności w produkcji. Analizując wariancję wyników produkcji, menedżerowie mogą dostrzec, które linie produkcyjne mają większe odchylenia od normy, co może wskazywać na problemy z jakością lub procesem. Dzięki tym informacjom można wprowadzić odpowiednie zmiany, aby zredukować zmienność i poprawić efektywność operacyjną.
Dodatkowo, w kontekście analizy ryzyka, wariancja może pomóc w ocenie stabilności finansowej projektów. Im wyższa wariancja przewidywanych kosztów, tym większe ryzyko przekroczenia budżetu. Firmy mogą zastosować tę wiedzę do lepszego planowania finansowego, co pozwala na bardziej świadome decyzje inwestycyjne. W ten sposób, umiejętne wykorzystanie wariancji w analizie danych może prowadzić do znaczących oszczędności i zwiększenia rentowności.